I got an antibody test. What does it mean?

by James Chenoweth, MD MAS

Disclaimer: I am not a statistician. I studied biostatistics during my master's program and have continued to study interpretation of medical research. I have avoided fractional positive/negative rates because they cause confusion and do not change the general principles discussed. Each test has its own test statistics and you should review those to help you interpret your results.

There has been a lot of recent focus on antibody testing for possible prior infection with SARS-CoV-2. Non-random sampling of several populations has suggested that the numbers of confirmed cases may be significantly undercounting the actual number of infections.  If true, this could be good news. For one, it would suggest that the actual mortality number may be markedly lower than the current case fatality rates. It would also mean that a portion of the population could now be immune. However, before we get too excited, I think it is important to understand what these tests really are telling us, how accurate they are, and how underlying disease prevalence plays a role when interpreting the tests.

What are we looking for?

Let’s tackle the first question, what do these tests mean? In brief, no one really knows. We have just begun to study the natural course of infection with SARS-CoV-2 and don’t yet understand how long these antibodies stay around or if they confer immunity. I suspect that, like other coronaviruses, it will depend on the antibody titer and not a simple yes/no test.

Many tests look for both IgM and IgG antibodies. IgM is the first antibody produced by the body in response to an infection, typically 3-7 days for COVID-19 infection. IgG is produced later, starting around 14 days after initial infection, and is also the antibody type that often (but not always) suggests a person is immune to infection. If we use hepatitis A testing as an example, presence of IgM would suggest current infection while presence of IgG may represent current infection, recent infection, or immunity (if the antibody being tested for is a neutralizing antibody). Unfortunately, in the case of SARS-CoV-2, we do not know when these antibodies begin to be detectable or how long they stick around. If it behaves like other coronavirus infections, immunity will likely wane over the course of months to a few years.

Test Characteristics

Now we can move on to how accurate these tests are. Not all tests are created equal, particularly under the looser requirements of FDA emergency use authorization which is not synonymous with approval. From what limited information is available in the FDA Emergency Use Authorizations, it seems that most laboratory-based tests have a sensitivity of ~90% and a specificity of ~99%. What do these numbers mean? Buckle up, it’s time to discuss test statistics. For people who prefer a visual representation, I’ve attached what’s called a 4x4 table. The 4x4 table contains all the data we need to calculate the test performance characteristics and contains 4 quadrants: true positives, false positives, false negatives, and true negatives. To determine who actually had the disease a test must be compared against a gold standard. In the case of SARS-CoV-2, the gold standard is detection of viral RNA.

	Disease +	Disease -
Test +	True Positive (A)	False Positive (C)	All Test +
Test -	False Negative (B)	True Negative (D)	All Test -
	All Disease +	All Disease -

We’ll start with Sensitivity. Sensitivity is calculated by dividing the true positives by all people with a disease (A/A+B). This tells you the probability that a person will test positive in they have a disease. Tests with very high sensitivity are best used as screening tests because they have very few false negatives. In the case of SARS-CoV-2 antibody test, a sensitivity of 90% means that 10% of people who previous had a prior SARS-CoV-2 infection will still test negative.

Now we can look at specificity. Specificity is calculated by dividing true negatives by all negative tests (D/C+D). This result tells you the probability that a person without the disease will test negative. Highly specific tests are often used as confirmatory tests because they very rarely identify people without the disease as positive. For SARS-CoV-2, the antibody test has a specificity of ~99% which means that only 1% of tests performed on people who were never infected will be positive (a false positive test).

With this information, you can also calculate things like the positive and negative predictive value. In reality, this information is more useful from a clinical perspective because it takes into account the prevalence of infection in a population. Performance characteristics will vary based on prevalence of disease in a population. Positive predictive value is the percent of positive tests that are true positives (A/A+C) while negative predictive value is the percent of negative tests that are true negatives (D/B+D). The real problem is that we don’t know what the real prevalence is in our population. Instead, we are performing a circular process where we use a test to determine the prevalence that then lets us know how accurate the test is.

Disease prevalence and test interpretation

How important is disease prevalence? To understand how this affects interpreting test results lets do a couple hypothetical examples in 3 different populations, one with 1% prevalence of current or previous infection with SARS-CoV-2, one with 10% infection, and one with 20% infection.

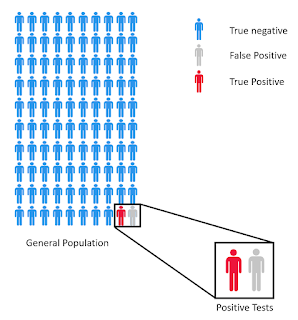In the 1% prevalence case, a negative test ends up being relatively good. With a 90% sensitivity you expect around 10% of people with the infection to have a false negative. A little math shows that if you run 1000 tests you would be expected to have tested 10 people with the disease. If 10% have a false negative, then that means 1 of 1000 negative tests will be a false negative.  Not too bad. The opposite is true for a positive test. Even at 99% specificity, out of 100 tests on people without prior infection will be a false positive.  In this population, if you test 100 people you would expect 1 true positive and 1 false positive, meaning that even if your test is positive, it is a coin flip as to whether that actually means you had previous infection with SARS-CoV-2.




                                                  1% disease prevalence (1000 individuals tested)

	Disease +	Disease -
Test +	9	10	19
Test -	1	980	981
	10	990

Now we go to the 10% prevalence population. In this group you would expect 10 positives for every 100 tests performed. With 90% sensitivity, at least 1 of these 10 could result in a false negative. This is still not horrible with 1% of negative tests being a false negative.  With the positive tests we see significant improvement with ~1 false positive test for every 9 true positives (1 person with previous infection will be a false negative so this is subtracted from the 10 with previous infection). In this population your positive test is better with only a 10% chance of your test being a false positive.

                                                  10% disease prevalence (100 individuals tested)

	Disease +	Disease -
Test +	9	1	10
Test -	1	89	90
	10	90

In the 20% infection population (which has been reported in NYC) you expected 20 positives for every 100 tests. Using the same test characteristics, you would expect 2 of these to result in false negatives meaning that ~2% of negative tests will be false negatives. The positive test is better, however. For every 100 tests you would get 18 true positives and 1 false positive meaning that only 5.5% of positive tests are false positives.

                                                  20% disease prevalence (100 individuals tested)

	Disease +	Disease -
Test +	18	1	19
Test -	2	79	81
	20	80

What does this all mean for your results? Its hard to say. At a minimum you can put a floor on prevalence with the number of confirmed cases in your area. In most regions, a negative test puts you at <1% chance of having had SARS-CoV-2. The real questions arise with positive tests and a question of whether a singe test provides any real information and concerns about false reassurance. I would argue that unless you live in NYC or another hard-hit area, the answer is no. So, what can you do? The answer is serial testing.

The importance of serial or confirmatory testing

Let’s go back to the 1% prevalence population. If you have a positive test, then you are put into a new population, specifically those with positive tests. This new population (those with positive tests) has a disease prevalence of 50%. In this population for every 100 tests you would expect 5 false negatives, 0.5 false positive, and 45 true positives. So only ~1% of positive tests are false positives.

You can go down this rabbit hole as far as you want, playing with different prevalence rates and doing the calculations. The point is that we are missing some very important baseline information which means that even random sampling has potential to greatly overestimate the real disease prevalence due to false positives. This not only affects the interpretation of future tests, but also risks falsely reassuring people who get a positive result.

In most situations in medicine, screening tests are designed to be highly sensitive. You get as few false negatives as possible and in the process, you increase the disease prevalence in your testing subpopulation (ie those testing positive). You then use a highly specific test to confirm infection. Because you have already weeded out a large portion of people without the disease, any further positive tests are more likely true positives. That is not the approach currently being taken. The only real answer is serial testing of every positive (and possibly every negative). Unfortunately, this isn’t feasible given our current testing capabilities.